[rgb이미지의 2d 콘볼루션은 3d콘볼루션으로 작용한다][convolution kernel의 깊이(depth)는 생략되어 있다]convolution 연산에서 입력영상의 컬러채널 또는 다수의 깊이(depth channel)채널과 필터의 콘볼루..
Deep Learning 2021. 4. 15. 11:18결론은 summation across chaannel이다. 각 채널별로 콘볼루션 계산 후 더하여 output을 만든다.
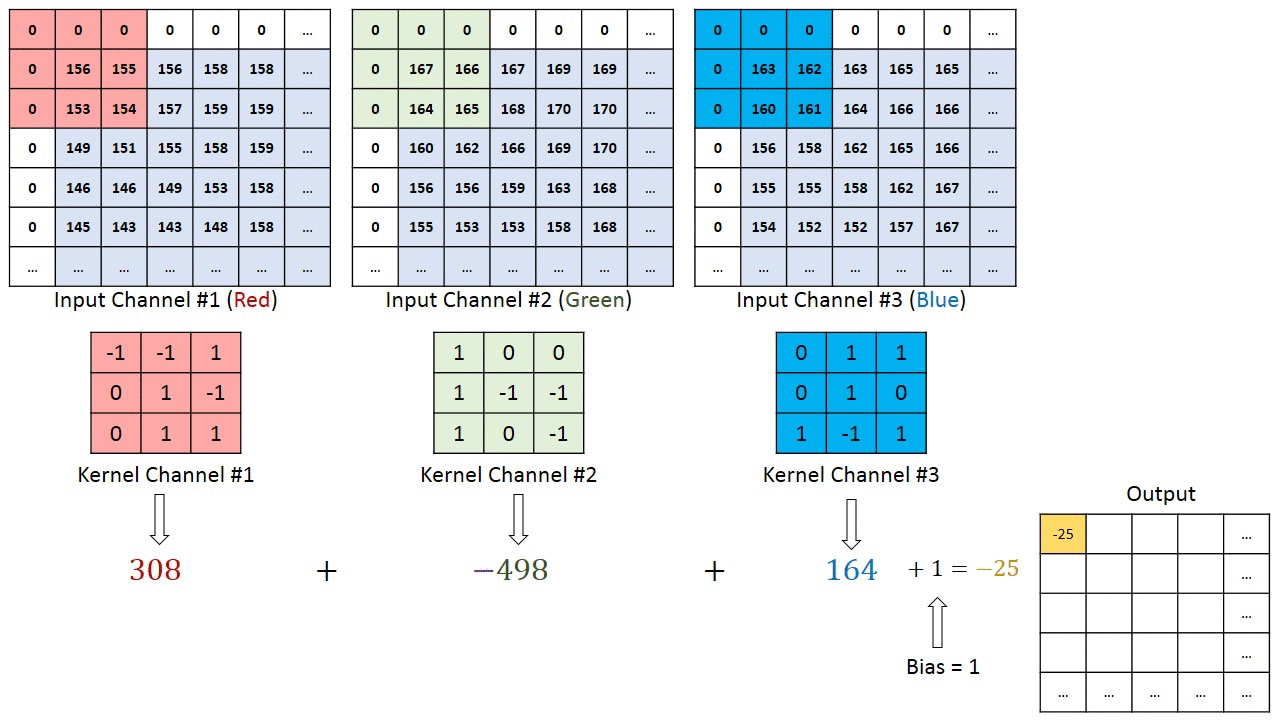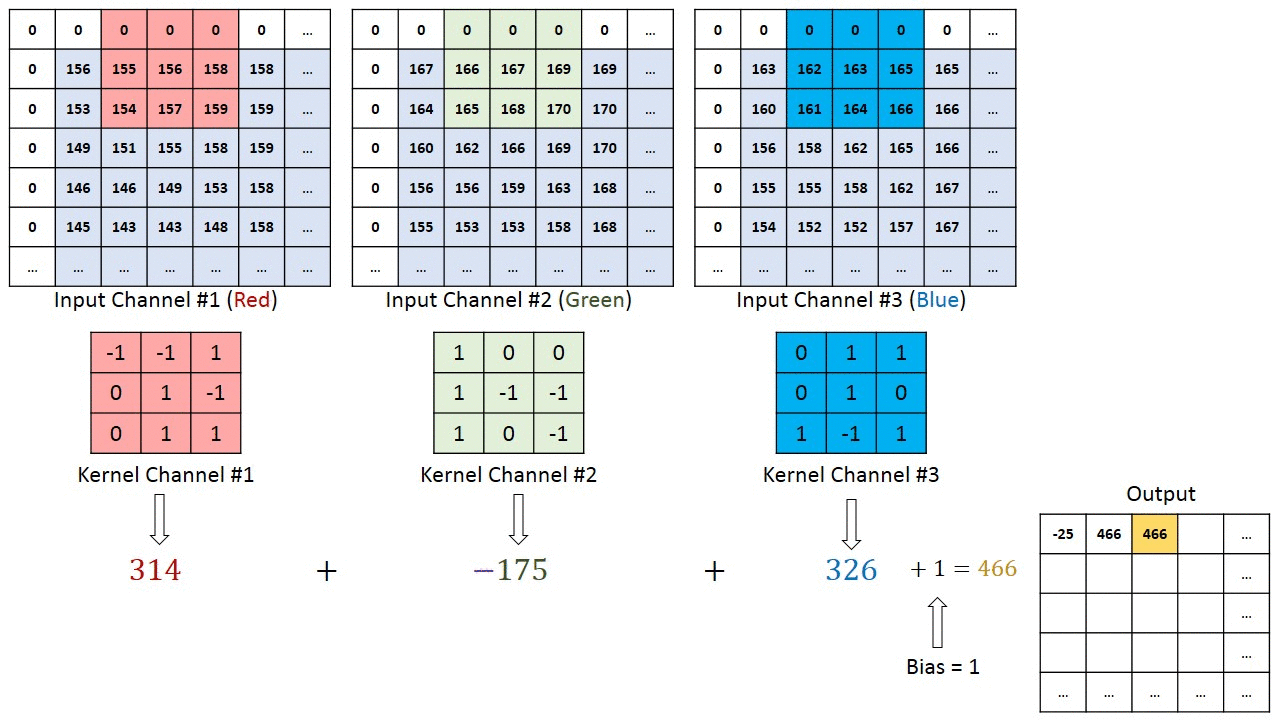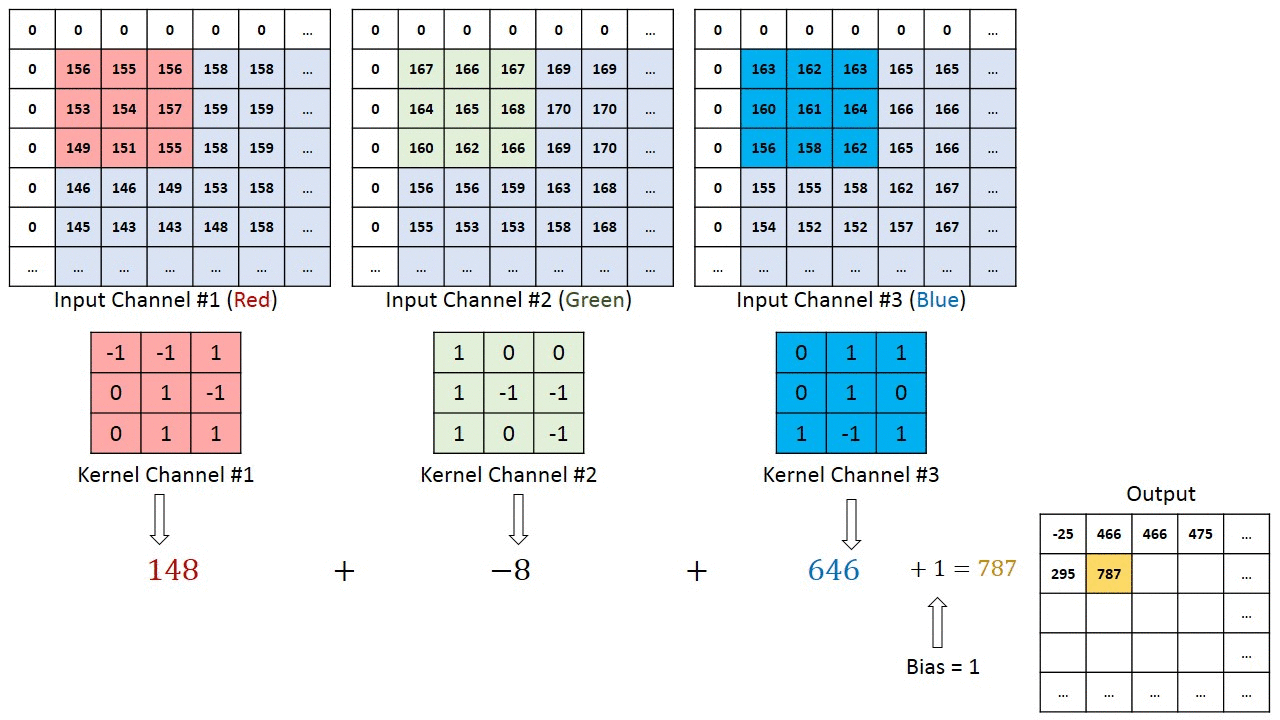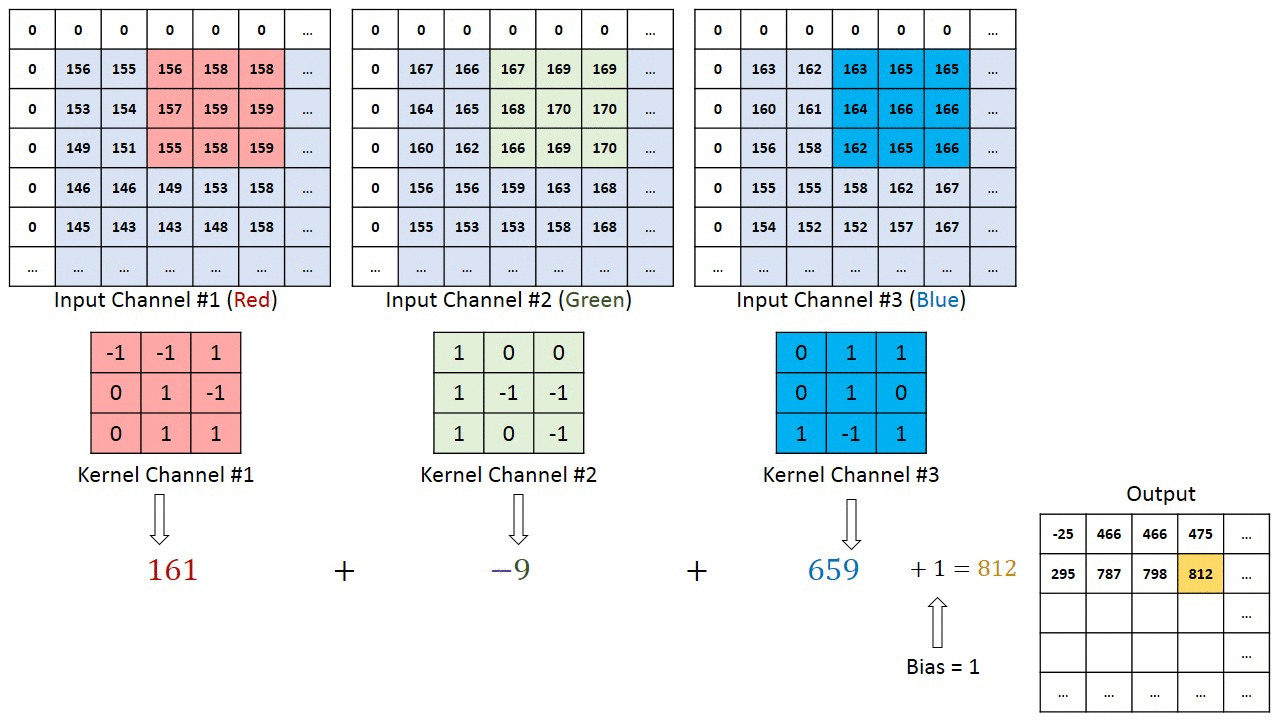
[1] https://stackoverflow.com/questions/43306323/keras-conv2d-and-input-channels
[2] https://datascience.stackexchange.com/questions/76456/why-do-we-use-2d-kernel-for-rgb-data
----------------------------------------------------------------------------------------------------------------
[1] stackoverflow.com/questions/43306323/keras-conv2d-and-input-channels
Keras Conv2D and input channels
The Keras layer documentation specifies the input and output sizes for convolutional layers: https://keras.io/layers/convolutional/
Input shape: (samples, channels, rows, cols)
Output shape: (samples, filters, new_rows, new_cols)
And the kernel size is a spatial parameter, i.e. detemines only width and height.
So an input with c channels will yield an output with filters channels regardless of the value of c. It must therefore apply 2D convolution with a spatial height x width filter and then aggregate the results somehow for each learned filter.
What is this aggregation operator? is it a summation across channels? can I control it? I couldn't find any information on the Keras documentation.
- Note that in TensorFlow the filters are specified in the depth channel as well: https://www.tensorflow.org/api_guides/python/nn#Convolution, So the depth operation is clear.
Thanks.
Follow
asked Apr 9 '17 at 11:46

1,5584 gold badges15 silver badges24 bronze badges
- 1
- You need to read this. – Autonomous Apr 9 '17 at 22:27
- From this page: "In the output volume, the d-th depth slice (of size W2×H2) is the result of performing a valid convolution of the d-th filter over the input volume with a stride of SS, and then offset by d-th bias. ". So I still don't follow how these convolutions of a volume with a 2D kernel turn into a 2D result. Is the depth dimension reduced by summation? – yoki Apr 10 '17 at 6:53
- 1
- "Example 1. For example, suppose that the input volume has size [32x32x3], (e.g. an RGB CIFAR-10 image). If the receptive field (or the filter size) is 5x5, then each neuron in the Conv Layer will have weights to a [5x5x3] region in the input volume, for a total of 5*5*3 = 75 weights (and +1 bias parameter). Notice that the extent of the connectivity along the depth axis must be 3, since this is the depth of the input volume." - I guess you are missing it's 3D kernel [width, height, depth]. So the result is summation across channels. – Nilesh Birari Apr 10 '17 at 11:21
- 1
- @Nilesh Birari , my question is exactly how to know what Keras is doing. I guess it's summation, but how can I know for sure? – yoki Apr 10 '17 at 11:54
3 Answers
38
It might be confusing that it is called Conv2D layer (it was to me, which is why I came looking for this answer), because as Nilesh Birari commented:
I guess you are missing it's 3D kernel [width, height, depth]. So the result is summation across channels.
Perhaps the 2D stems from the fact that the kernel only slides along two dimensions, the third dimension is fixed and determined by the number of input channels (the input depth).
For a more elaborate explanation, read https://petewarden.com/2015/04/20/why-gemm-is-at-the-heart-of-deep-learning/
I plucked an illustrative image from there:

Follow
answered Jul 12 '17 at 10:26

5,4357 gold badges37 silver badges61 bronze badges
- 4
- So do each channel of the filter have their own weights which can be optimized? Or do we just compute the weights for one channel and use that as values for the rest of the channels of the filter. – Moondra Nov 20 '17 at 23:02
- 1
- The kernels are different for all channels. See my answer. – Alaroff May 24 '18 at 7:42
- I think different kernels are used only for illustration. In Keras it may be implemented with same Kernel across channels. – Regi Mathew May 29 '19 at 6:29
Report this ad
34
I was also wondering this, and found another answer here, where it is stated (emphasis mine):
Maybe the most tangible example of a multi-channel input is when you have a color image which has 3 RGB channels. Let's get it to a convolution layer with 3 input channels and 1 output channel. (...) What it does is that it calculates the convolution of each filter with its corresponding input channel (...). The stride of all channels are the same, so they output matrices with the same size. Now, it sums up all matrices and output a single matrix which is the only channel at the output of the convolution layer.
Illustration:
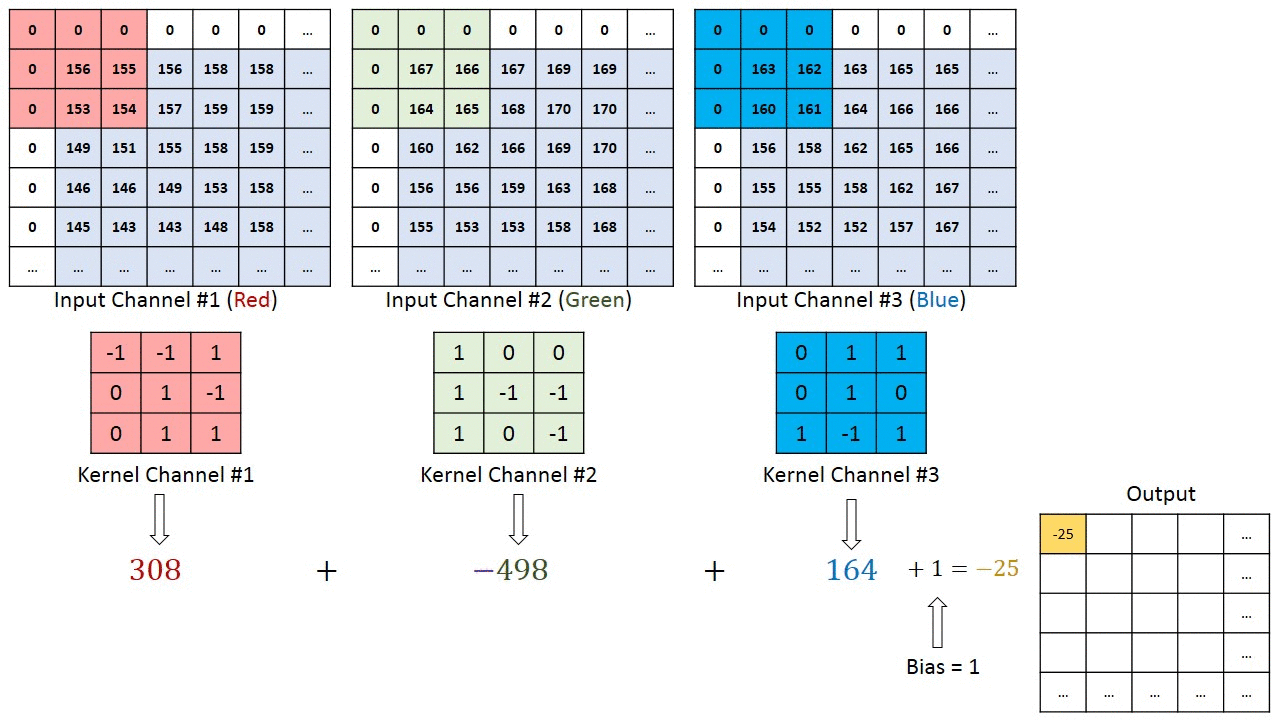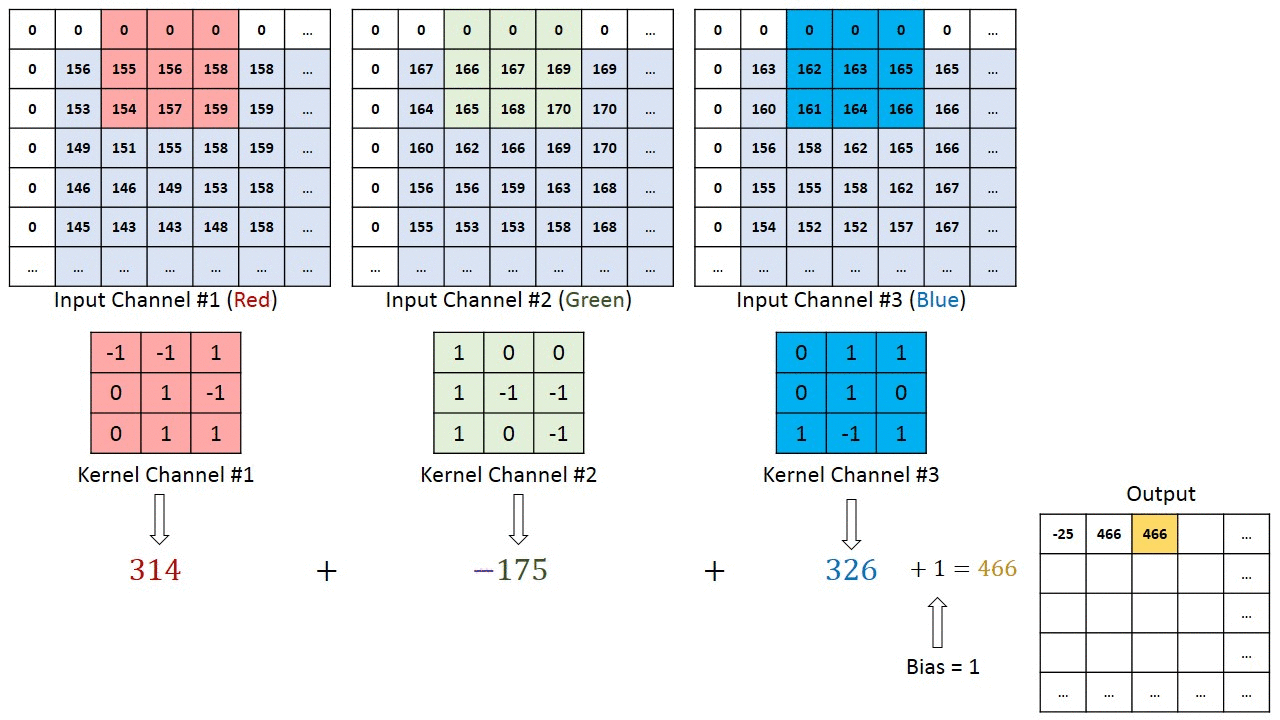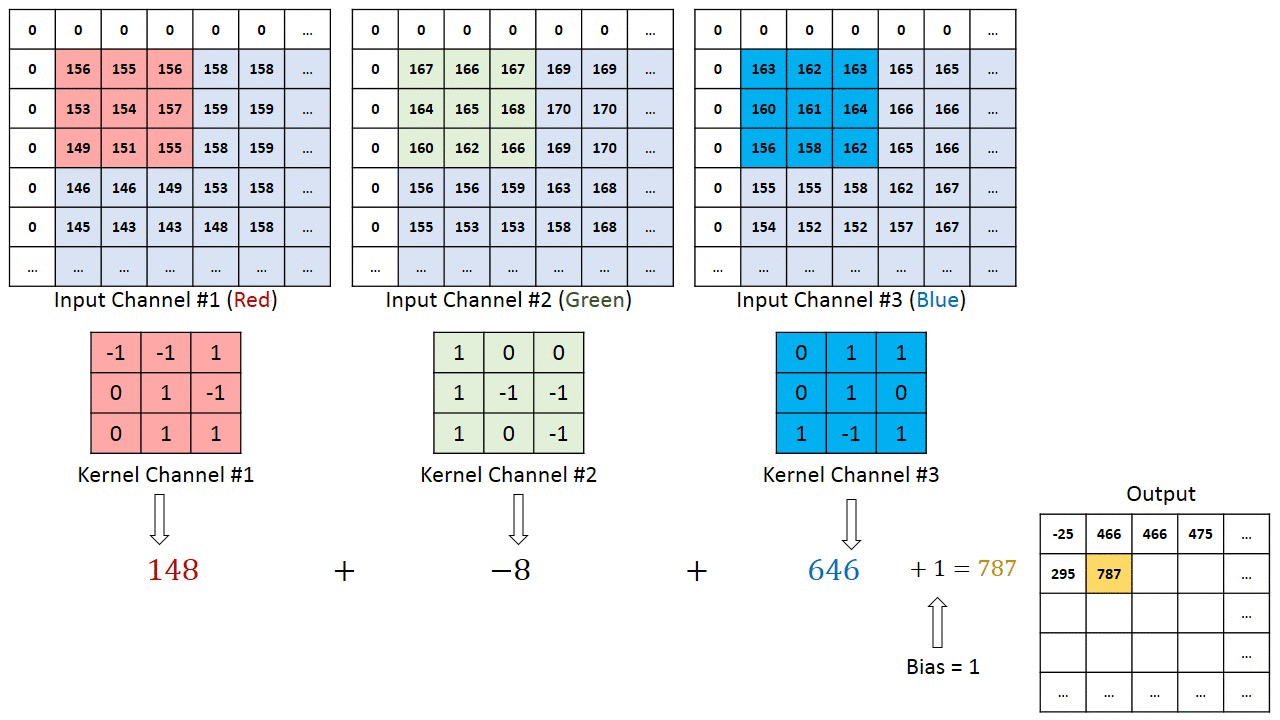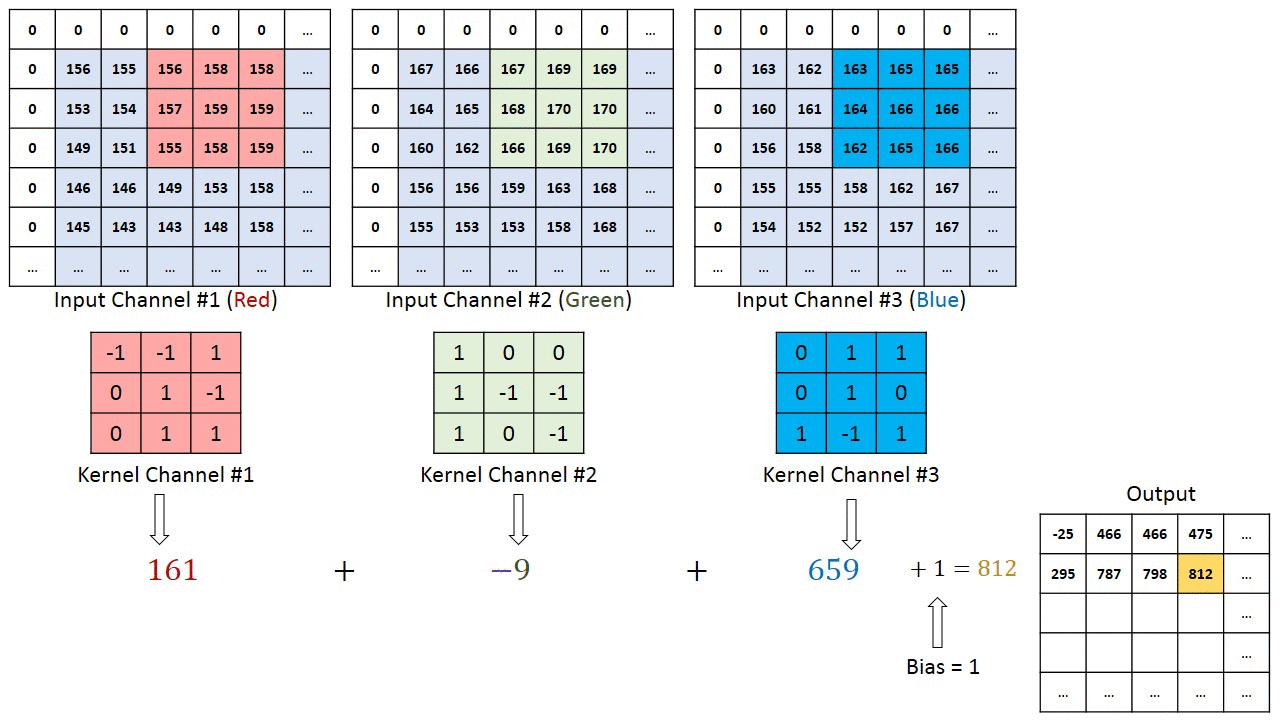
Notice that the weights of the convolution kernels for each channel are different, which are then iteratively adjusted in the back-propagation steps by e.g. gradient decent based algorithms such as stochastic gradient descent (SDG).
Here is a more technical answer from TensorFlow API.
Follow
answered May 13 '18 at 14:36

1,52511 silver badges9 bronze badges
28
I also needed to convince myself so I ran a simple example with a 3×3 RGB image.
# red # green # blue 1 1 1 100 100 100 10000 10000 10000 1 1 1 100 100 100 10000 10000 10000 1 1 1 100 100 100 10000 10000 10000
The filter is initialised to ones:
1 1 1 1
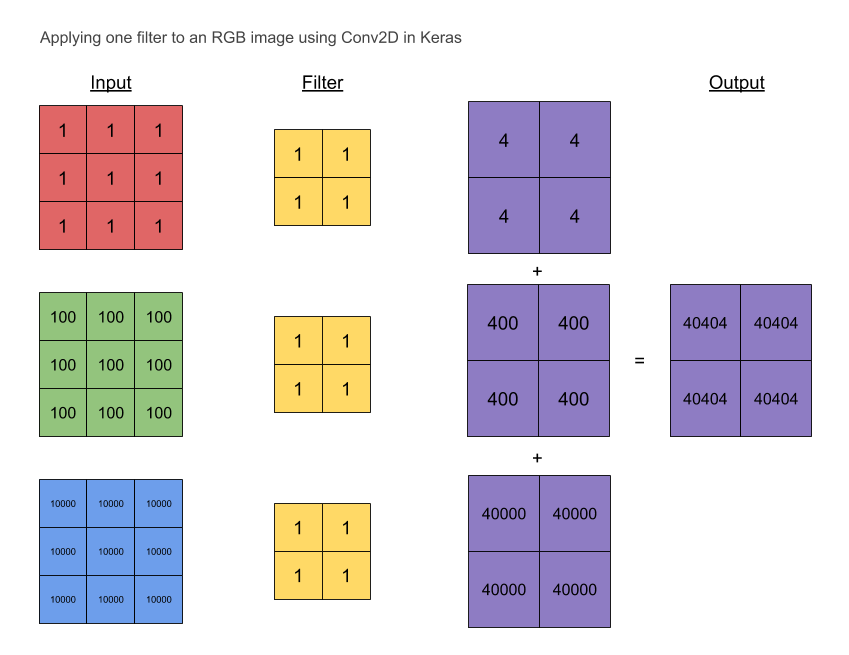
I have also set the convolution to have these properties:
- no padding
- strides = 1
- relu activation function
- bias initialised to 0
We would expect the (aggregated) output to be:
40404 40404 40404 40404
Also, from the picture above, the no. of parameters is
3 separate filters (one for each channel) × 4 weights + 1 (bias, not shown) = 13 parameters
Here's the code.
Import modules:
import numpy as np from keras.layers import Input, Conv2D from keras.models import Model
Create the red, green and blue channels:
red = np.array([1]*9).reshape((3,3)) green = np.array([100]*9).reshape((3,3)) blue = np.array([10000]*9).reshape((3,3))
Stack the channels to form an RGB image:
img = np.stack([red, green, blue], axis=-1) img = np.expand_dims(img, axis=0)
Create a model that just does a Conv2D convolution:
inputs = Input((3,3,3)) conv = Conv2D(filters=1, strides=1, padding='valid', activation='relu', kernel_size=2, kernel_initializer='ones', bias_initializer='zeros', )(inputs) model = Model(inputs,conv)
Input the image in the model:
model.predict(img) # array([[[[40404.], # [40404.]], # [[40404.], # [40404.]]]], dtype=float32)
Run a summary to get the number of params:
model.summary()

Follow
answered Dec 26 '18 at 9:37

1,43717 silver badges22 bronze badges
- 3
- EXCELLENT contribution – Regi Mathew May 29 '19 at 6:20
- 4
- This is an excellent answer. Honestly I think the name conv2d is very confusing. – jelmood jasser Aug 19 '19 at 3:29
- So, I am not the only one who started to wonder what's actually happening there and what does the underlying aggregation look like? – Stefan Falk Jul 23 '20 at 14:01
[2] https://datascience.stackexchange.com/questions/76456/why-do-we-use-2d-kernel-for-rgb-data
I have recently started kearning CNN and I coukdnt understand that why are we using a 2D kernel like of shape (3x3) for a RGB data in place of a 3D kernel like of shape (3x3x3)?
Are we sharing the same kernel among all the channels because the data would look the same in all the channels?
-->
welcome to the community
I guess there's a confusion in your understanding of the kernel we use in case of rgb data. We normally use a kernel of equal number of channels as the input coming in (in this case as you mentioned it's RGB, so my number of channels for convolution operation would be 3). So instead of using a 3 X 3 Kernel, we use a 3 X 3 X 3 kernel. Weight matrix multiplication of kernel and image pixels happen channel-wise.
However, having said this, you can use a kernel of size 3 X 3 when input image is rgb, by specifying the stride as 1 in the third dimension. What this will do is convolute the kernel not only horizontally and vertically but also through the depth or specifically through the channels as well. I don't exactly know why one would like to do it.
Apart from this I guess the course or the video you are referring to might have specified '2D convolution on a 3D image'. That doesn't mean using a 2D kernel. And a 2D convolution on a 3D image uses a 3D kernel and after weight matrix multiplication you get a 2D image hence justifying the 2D convolution name.
'Deep Learning' 카테고리의 다른 글
| [arxiv.org에 올라온 논문을 pdf가 아닌 잘 정돈된 1 column의 텍스트 페이지로 볼 수 있는 방법] 주소 창에서 arxiv의 x를 숫자 5로 바꾸면 pdf가 아닌 텍스트 페이지로 나옴 (0) | 2022.10.17 |
|---|---|
| NVIDIA Research Unveils Flowtron, an Expressive and Natural Speech Synthesis Mod (0) | 2020.05.15 |
| 수학을 포기한 직업 프로그래머가 머신러닝 학습을 시작하기위한 학습법 소개 (0) | 2017.07.27 |
| 파이썬 쥬피터를 이용한 텐서플로우 개발환경 구성하기 (0) | 2017.04.13 |
| Why Momentum Really Works (0) | 2017.04.05 |



