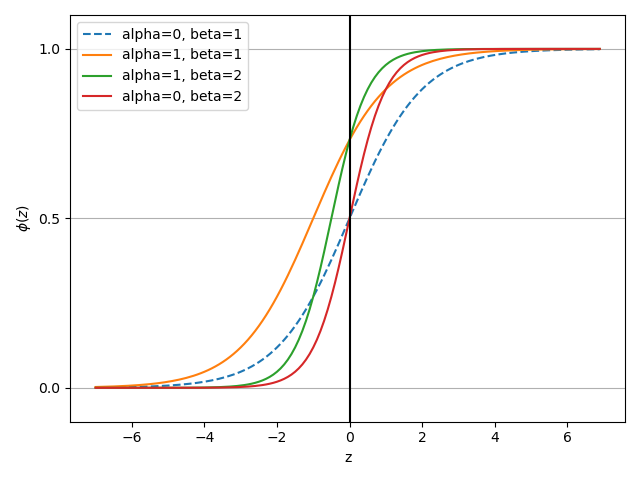
phi(z) = 1 / (1 + e^-(alpha + beta*z)) 일 때 다양한 alpha, beta에 따른 logistic function plot.
import matplotlib.pyplot as plt
import numpy as np
def sigmoid1(x, alpha, beta):
return 1.0 / (1.0 + np.exp(-(alpha + beta*x)))
z = np.arange(-7, 7, 0.1)
# phi_z = sigmoid1(alpha=3, beta=2, z)
c0 = [sigmoid1(x, alpha=0, beta=1) for x in z]
plt.plot(z, c0, label='alpha=0, beta=1', linestyle='--')
c1 = [sigmoid1(x, alpha=1, beta=1) for x in z]
plt.plot(z, c1, label='alpha=1, beta=1')
c2 = [sigmoid1(x, alpha=1, beta=2) for x in z]
plt.plot(z, c2, label='alpha=1, beta=2')
c3 = [sigmoid1(x, alpha=0, beta=2) for x in z]
plt.plot(z, c3, label='alpha=0, beta=2')
plt.axvline(0.0, color='k')
plt.ylim(-0.1, 1.1)
plt.xlabel('z')
plt.ylabel('$\phi (z)$')
# y축의 눈금과 격자선
plt.yticks([0.0, 0.5, 1.0])
ax = plt.gca()
ax.yaxis.grid(True)
plt.legend(loc='best')
plt.tight_layout()
plt.show()


